La determinación de la energía de enlace nos sirve para predecir si una reacción es exotérmica o endotérmica dependiendo de la estabilidad de las moléculas en reactivos y productos y considerando que la ruptura de enlaces requiere energía y la formación de nuevos enlaces, desprendimiento.
Muchas veces, como vimos anteriormente, no es posible determinar con exactitud las entalpías de enlace de moléculas poliatómicas, debido a la diversidad de condiciones químicas que se presentan y sólo podemos obtener cálculos aproximados de las entalpías.
Resulta más conveniente calcular la variación de la entalpía de reacción, a partir de las entalpías estándares de formación de reactivos y productos. La entalpía estándar de formación ∆H0f, es el cambio de energía que se produce cuando un mol de un compuesto se forma a partir de sus elementos, a presión de una atmósfera y temperatura de 25 oC. El exponente 0 nos indica estas condiciones de presión y temperatura, las que se conocen, como condiciones estándares.
Estas entalpías se calculan experimentalmente en un calorímetro a presión constante y por convención, a los elementos que existen en más de una forma en condiciones estándares, la más estable, tiene una entalpía de formación igual a cero.
El oxígeno, existe como: O, O2 y O3. La forma más estable a 25 oC y 1 atmósfera de presión es el O2, su entalpía de formación es cero.
Si se conocen las entalpías estándares de formación de reactivos y productos, se puede calcular la entalpía estándar de reacción ∆H0r, con más exactitud.
Si se tiene una reacción:
aA + bB → cC + dD
La entalpía estándar de reacción, está dada por:
∆H0r = ∑∆H(productos) - ∑∆H(reactivos)
En donde:
∑∆H(reactivos) = [ a∆H0f de A + b∆H0f de B ]
∑∆H(productos) = [ c∆H0f de C + d∆H0f de D ]
a, b, c, y d corresponden al número de moles de A, B, C y D.
La entalpía estándar de formación para un mismo compuesto, es diferente en cada una de las fases en las que se presente.
La entalpía estándar de formación para el:
H2O(l) = -285.8 kJ/mol y para el H2O(g) = -241.8 kJ/mol
Los cambios de entalpía que se producen en las reacciones químicas se pueden determinar por:
El método directo. Este método se utiliza cuando las reacciones químicas se completan de manera sencilla, sin productos secundarios que interfieran en la determinación de la entalpía estándar de formación en un calorímetro a presión constante. Las reacciones de combustión son un ejemplo de reacciones que ocurren con limpieza.
Los valores obtenidos de las entalpías de formación ∆H0f, están reportados en tablas y nos sirven para determinar la entalpía de reacción a partir de ellos empleando la ecuación anterior. Encontrarás la tabla de datos termodinámicos al final de esta sección.
Calcular las entalpías de reacción para las siguientes reacciones químicas:
1. C(grafito) + O2(g) → CO2(g)
C(grafito) + O2(g) → CO2(g)
∆Hf = 0 ∆Hf = 0 ∆Hf = -393.5 kJ/mol
Para los reactivos:
∑∆H0f (reactivos) = [ 1molx0 + 1molx0 ] = 0
Para los productos:
∑∆H0f (productos) = [ 1molx(-393.5 kJ/mol) ] = -393.5 kJ
∆H0r = ∑∆H(productos) - ∑∆H(reactivos)
∆H0r = -393.5 kJ – ( 0 kJ)
∆H0r = -393.5 kJ
∆H0r < 0 Reacción exotérmica
2. C2H6(g) + 3 1/2O2(g) → 2CO2(g) + 3H2O(g)
C2H6(g) + 3 1/2O2(g) → 2CO2(g) + 3H2O(g)
∆Hf = -84.7 kJ ∆Hf = 0 ∆Hf = -393.5 kJ/mol ∆Hf = -241.8 kJ
Para los reactivos:
∑∆H0f (reactivos) = [ 1molx(-84.7 kJ) + 3 1/2molx0 ] = -84.7 kJ
Para los productos:
∑∆H0f (productos) = [ 2molx(-393.5 kJ/mol) + 3(-241.8 kJ) ] = -1512.4 kJ
∆H0r = ∑∆H(productos) - ∑∆H(reactivos)
∆H0r = -1512.4 kJ – ( -84.7 kJ)
∆H0r = -1427.7 kJ
∆H0r < 0 Reacción exotérmica
Calcular las entalpías de las siguientes reacciones y establecer si son exotérmicas o endotérmicas con base en los cálculos.
1. 6CO2(g) + 6H2O(l) → C6H12O6(s) + 6O2(g)
2. N2(g) + 3H2(g) → 2NH3(g)
3. C6H6(l) + 7 1/2O2(g) → 6CO2(g) + 3H2O(l)
El método indirecto, Ley de Hess. Este método tiene aplicación, cuando en las reacciones químicas se producen compuestos secundarios que no tienen interés, cuando se llevan a cabo con demasiada lentitud o los compuestos no se pueden sintetizar a partir de sus elementos, lo que imposibilita hacer una medición de manera directa de la entalpía, como en el método anterior.
En estas circunstancias, los cambios de entalpía se pueden calcular tomando valores de reacciones bien conocidas y aplicar La Ley de Hess.
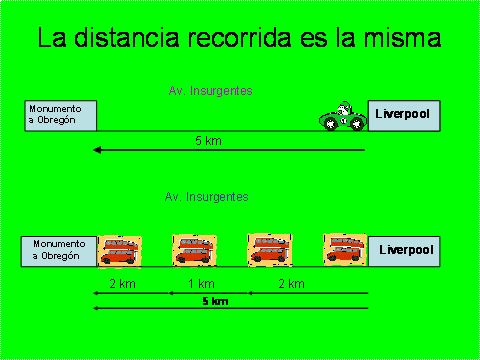
La Ley de Hess dice: Cuando en una reacción química los reactivos se convierten en productos, la variación de la entalpía es el mismo independientemente de que se verifique la reacción en un paso o en una serie de pasos. Esto significa que, si se separa una reacción en una serie de reacciones con valores de entalpía de reacción conocidos, se puede calcular ∆H0reacción para la reacción original.
Analogía. Si una persona se encuentra en Liverpool, en la Avenida Insurgentes, y necesita desplazarse al Monumento a Obregón que se encuentra en la misma avenida hacia el norte y consideramos que no existen semáforos, lo puede hacer de dos formas. Por la forma directa en automóvil sin hacer paradas y por el forma indirecta, tomando un microbús que realiza varias paradas para subir y bajar pasaje. En ambos casos, recorre la misma distancia.
Calcular la entalpía estándar de formación del metano.
Escribir la ecuación de síntesis del metano
C(grafito) + H2(g) → CH4(g)
Esta reacción no puede efectuarse como está escrita por lo que no es posible medir el cambio de entalpía de manera directa. En estos casos es cuando se hace uso del método indirecto y se aplica la ley de Hess.
Se parte de reacciones de combustión del C, H2 y CH4 para las que se conoce con exactitud los valores del cambio de entalpía de reacción. Se establece:
a) C(grafito) + O2(g) → CO2(g) ∆H0r = -393.5 kJ
b) 2H2(g) + O2(g) → 2H2O(l) ∆H0r = -571.6 kJ
c) CH4(g) + 2O2(g) → CO2(g) + 2H2O(l) ∆H0r = -890.4 kJ
La ecuación global sólo contiene C e H2 como reactivos y CH4 como producto. De acuerdo a la ley de Hess, se deben acomodar todas las ecuaciones químicas de tal manera que, al sumarlas se cancelen las especies que no aparecen en la ecuación original y únicamente permanezcan los reactivos y productos. Algunas veces es necesario multiplicar una o todas las ecuaciones por un coeficiente que permita eliminar las especies que no aparecen en la reacción de interés.
En las ecuaciones a) y b), tanto el C como el H2 están como reactivos, entonces permanecen como se escribieron. Sin embargo, el CH4 también se encuentra como reactivo, debe invertirse para quedar del lado de los productos. Al invertir una ecuación es muy importante cambiar el signo del valor de la entalpía de reacción, puesto que se debe considerar que si una reacción en un sentido es exotérmica (∆H0r = -), en el sentido contrario siempre es endotérmica (∆H0r = +).
Nota: Si una reacción en un sentido es exotérmica, en el sentido contrario es endotérmica y el valor de (∆H0r), en ambos procesos, es el mismo.
Se invierte la ecuación c) y se cambia el signo de ∆H0r:
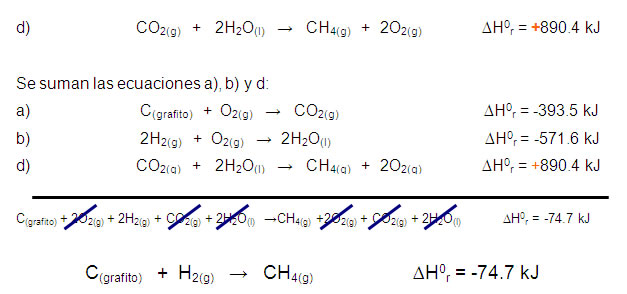
Calcular la entalpía estándar de formación del acetileno a partir de sus elementos.
La ecuación para la formación del acetileno es:
C(grafito) + H2(g) → C2H2(g)
Se establecen las ecuaciones de combustión para el C, H2 y C2H2 con sus cambios de entalpías:
a) C(grafito) + O2(g) → CO2(g) ∆H0r = -393.5 kJ
b) 2H2(g) + O2(g) → 2H2O(l) ∆H0r = -571.6 kJ
c) 2C2H2(g) + 5O2(g) → 4CO2(g) + 2H2O(l) ∆H0r = -2598.8 kJ
El C y el H2 se encuentran como reactivos, al igual que en la ecuación global, el C2H2 también está como reactivo por lo que se debe invertir la ecuación y quede como producto; no olvidar cambiar el signo de la entalpía para esta ecuación.
d) 4CO2(g) + 2H2O(l) → 2C2H2(g) + 5O2(g) ∆H0r = +2598.8 kJ
Para eliminar las especies que no intervienen en la ecuación global, es necesario multiplicar la ecuación a) por 4 para igualar el número de O2 y CO2 en ambos lados, el valor de la entalpía de reacción de esta ecuación, debe multiplicarse de la misma manera, por el mismo factor.
e) 4C(grafito) + 4O2(g) → 4CO2(g) ∆H0r = 4(-393.5 kJ) = -1574 kJ
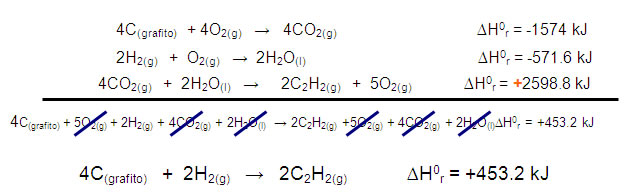
Para llegar a la ecuación global, la ecuación anterior se divide entre dos, sin olvidar la entalpía de reacción:
2C(grafito) + H2(g) → C2H2(g) ∆H0r = +226.6 kJ
Calcular las entalpías de formación para las siguientes reacciones:
1. C(grafito) + O2(g) → CO2(g) ∆H0r = -393.5 kJ
2. CS2(l) + 3O2(g) → CO2(g) + 2SO2(g) ∆H0r = -1072 kJ
Anterior Subtema 1.1 Siguiente
